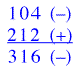This triplet relationship is known as the
Σ2 relationship. It postulates that if three large reflections
have hkl indices related as hkl, h'k'l' and h-h'k-k'l-l', the product of their signs (representing
the sign of |Fhkl| as +1 or -1) is “probably” equal to +1. The probability that the
Σ2 relation is correct for a particular reflection triplet is related to
the magnitudes of the three Fhkl's. If two phases in the triplet are known, the
Σ2 relationship can be used to calculate the phase of the third
reflection:
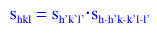For example, if the reflections 104, 212 and 316 are all “large” reflections and if the phase of
|F104| is known to be + and the phase of |F212| is -, the phase of
|F316| is probably - :
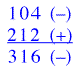(Notice that in this formulation, the indices of the reflection for which the phase is unknown are
the sums of the indices of the known reflections).
The Σ2 relationship is a very powerful tool for expanding a
small starting set of known phases to produce enough known phases to construct a recognizable Fourier
electron density map. But there are still two important questions to be dealt with:
What constitutes a “large” reflection?
How is that beginning set of known phases generated?
