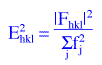The difficulty in defining a large reflection results from the drop-off in the scattering power of an atom with sinθ/λ:

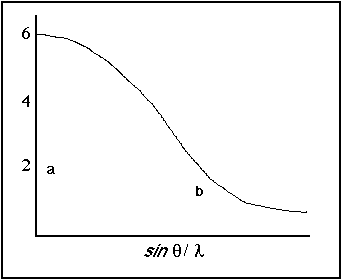
A low angle reflection may have a numerically larger |F_hkl| than a high angle reflection, but the high angle reflection may actually be using more of the “available” scattering power. Consider, for example, the two points on the scattering factor diagram above. Point “a” is a low angle reflection that doesn't “use” much of its available scattering power; “b” is a high angle reflection that uses a large proportion of its available scattering power. In this case, reflection “a” would have a numerically larger |F_hkl|, but reflection “b” is making more efficient use of it's scattering power. To remove these sinθ/λ effects, it is customary to calculate a normalized structure factor, E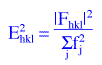_hkl: where the summation of f_j² is performed at the correct sinθ/λ for reflection hkl.