This analysis indicates that a Patterson map in space group P2₁/c will have three unique heavy atom vector peaks (“unique” in this context meaning “not related by the point group symmetry”): one peak at (0, ½ + 2y, ½) with a relative peak height of 2; another peak at (2x, ½, ½ + 2z) with a relative height of 2; and, a third peak at (2x, 2y, 2z) with relative height 1. (The relative peak heights are determined by the number of times that each vector is formed).
Below is a listing of the ten largest peaks in the Patterson map for the benzophenanthrene compound:

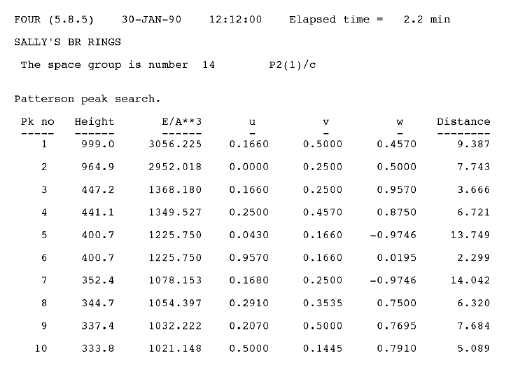
The list includes only unique Patterson peaks arranged from largest to smallest; the “distance” value is the distance in Å from the origin to the peak, so it is the length of the atom-atom vector resulting in that peak. Peak no. 1 (0.166, 0.500, 0.457) appears to be a peak of type (2x, ½, ½ + 2z); peak no. 2 appears to be (0, ½ + 2y, ½). These two peaks have approximately the same height (as would be expected - they both are formed twice in the vector grid analysis). It is unclear at this point which of the rest of the peaks is the (2x, 2y, 2z) type. Of course, peak no.1 and peak no. 2 could be assigned to either of the symmetry related Patterson peaks. Peak 1 could be assigned to be (2x, ½, ½ + 2z) or it could be (-2x, ½, ½ - 2z); the choice is arbitrary in the same sense as the choice of origin is arbitrary in choosing a unit cell.