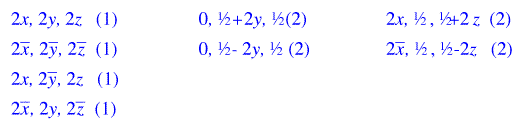The diagonal elements in this grid are vectors between atoms and “themselves”; thus, vectors of zero length are formed. (The superposition of these zero length vector peaks results in the large origin peak that is present in all Patterson maps). Also, wherever there might have been a coordinate of -½, these have been replaced by +½'s (i.e., the coordinates have been translated by +1 unit cell length).

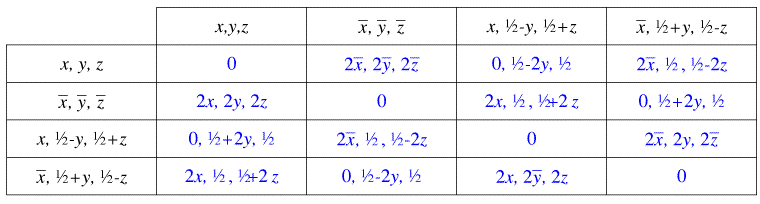
The resulting vector peaks fall into three classes (the numbers in parentheses are the no. of times a particular vector appears in the table):

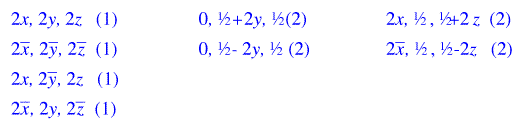The peaks in any one grouping are related by the symmetry of the Laue group, i.e., the point group plus a center of symmetry (if one isn't already present in the point group). The point group can be deduced from the space group by removing all translations from the space group symbol and from its symmetry related positions. Thus, for example, the first and third peaks in that first class of vector peaks are related by the mirror plane in point group 2/m that is perpendicular to the b-axis.