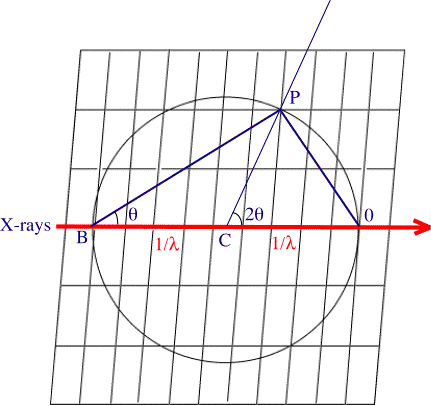
It is useful to develop a version of Bragg's Law in reciprocal space. In the diagram on the right, a circle of radius 1/λ has been drawn on a reciprocal lattice. The origin of the lattice is at 0; the crystal is at C; the X-ray beam is along the 0CB direction; lattice point P is on the circumference of the circle; the angle 0BP is labeled as θ. The triangle 0-B-P-0 is inscribed in a circle and therefore the angle 0PB is a right angle. The angle BCP is 180° - 2θ (the triangle B-C-P-B is an isosceles triangle because two of the sides are equal to 1/λ). Thus, the angle 0CP is 2θ.
The length of OP is 1/d_hkl (OP is the vector from the origin to reciprocal lattice point hkl); the length of OB is 2/λ (OB is the diameter of the circle). Finally, sinθ = OP/OB and, thus, sinθ = λ/2d_hkl which is just Bragg's Law rearranged: 2d_hkl sinθ = λ.
Using this construction, if a crystal is rotated about the origin of the reciprocal lattice, 0, whenever a lattice point comes into contact with the “circle of reflection”, Bragg's Law is fulfilled and a reflection occurs. The direction of the reflected beam is along CP (the angle between the direct beam and the reflected beam is 2θ).