Assuming, for the time being, that the relationship between the adjustable parameters (x, y, z plus temperature factors) and the calculated quantity (F_hkl) is linear, the method of least squares could be utilized to calculate the best values of the parameters. The relationship is certainly not linear (the adjustable parameters appear in exponential terms!), but it is useful to see how least squares might be applicable and then make an approximation that causes the relationship in the F_hkl expression to be treatable as linear.
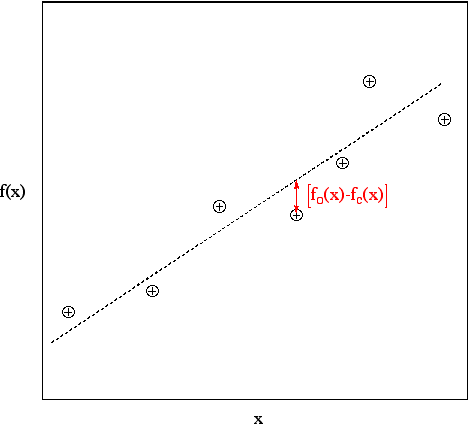
To recap the method of least squares, below is a graph of experimental points and the "best" straight line drawn through the points:

The principle of least squares postulates that the best straight line relating experimental data is obtained if the sum of the square of the differences between the observed quantity (the experimental data points) and the calculated quantity (located directly on the best straight line) is minimized. Thus, in the notation of the above graph the quantity minimized, D, is: